Discrete Fourier Transform

Discrete Fourier Transform (DFT) atau juga disebut Transformasi Fourier Diskrit merupakan suatu teknik dalam matematika untuk mengubah nilai sekuen atau urutan nilai diskrit tertentu dalam periode tertentu pada domain waktu ke domain frekuensi. DFT bertujuan untuk membawa nilai sinyal kontinyu (analog) untuk dijadikan nilai diskrit agar dapat diproses atau dilakukan perhitungan secara digital menggunakan mikrokontroler atau komputer.

Saat penulis masih duduk dibangku kuliah, DFT merupakan salah satu materi kuliah yang sulit dan rumit, bahkan sudah belajarpun tetap saja tidak lulus ujian dan harus mengulang. Kemudian penulis mencoba memahami DFT bukan dari rumus dan cara penyelesaiannya, tetapi mencoba memahami maksud yang disampaikan oleh rumus DFT tersebut, dan akhirnya penulis berhasil memahami maksud dari rumus DFT. 

DFT bukan suatu rumus yang sulit dan relatif mudah dipahami serta penting untuk dipelajari kususnya bagi siapa saja yang mempunyai hobi elektronika atau berkecimpung dalam dunia elektronika, sehingga dengan media blog ini penulis berbagi pengalaman bagaimana cara memahami DFT sehingga dapat digunakan dalam kehidupan nyata (bukan hanya sekedar rumus matematika saja).

DFT sangat penting untuk dasar pengolahan sinyal digital. Salah satu contoh dasar penerapan DFT pada bidang elektronika adalah untuk mengetahui tegangan, frekuensi listrik beserta gangguannya (harmonisa), faktor daya (cos fi) dan konsumsi daya listrik melalui perhitungan DFT yang dilakukan mikrokontroler atau komputer. 

Secara umum DFT dapat melakukan beberapa hal berikut :

Mengubah nilai sinyal diskrit pada domain waktu menjadi nilai diskrit dalam domain frekuensi.

Sinyal pada domain waktu hanya dapat menunjukan sebuah sinyal saja yang mungkin bentuk sinyal tersebut tampak tidak beraturan. Bentuk tidak beraturan tersebut (tidak murni sinusoidal) menandakan bahwa terdapat sinyal lain dengan frekuensi yang berbeda dan mungkin juga amplitudo atau magnitude yang berbeda mengganggu sebuah sinyal sinusoidal tersebut seperti ditunjukan pada Gambar 1.

Gambar 1. Ilustrasi penjumlahan benerapa sinyal sinusoidal

Gambar 1 menunjukan bahwa sebuah sinyal sinusoidal dengan frekuensi fundamental f1 mendapat gangguan 2 buah sinyal f2 dan f3 sehingga menghasilkan sebuah sinyal yang terlihat gambar ft dengan bentuk tidak beraturan dimana terlihat mirip dengan sinyal f1 tetapi bentuknya menjadi tidak beraturan. 

Hal yang perlu dipahami pada DFT adalah sinyal kontinyu atau sinyal analog pada domain waktu perlu diubah terlebih dahulu menjadi sinyal diskrit pada domain waktu dimana diambil nilainya pada titik tertentu pada suatu sinyal sepanjang waktu tertentu yang umumnya sering disebut sebagai sampel.

DFT mampu mengetahui magnitude frekuensi-frekuensi pengganggu pada sebuah sinyal, atau mampu mengetahui magnitude banyak frekuensi pada suatu sinyal dimana hal ini sulit dilakukan pada domain waktu.

Hasil perhitungan DFT pada sinyal ft Gambar 1 dapat membedakan atau memisahkan semua frekuensi yang berada pada sinyal ft   tersebut dengan menampilkan spektrum masing-masing sinyal seperti pada Gambar 2.

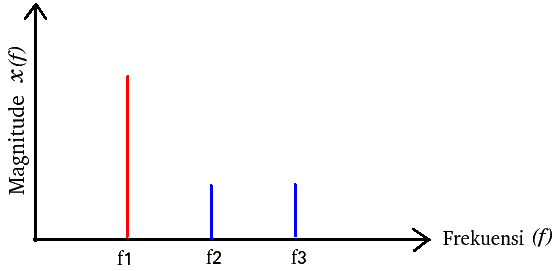Gambar 2. Spektrum sinyal hasil perhitungan DFT

f1 memiliki frekuensi lebih rendah dibanding f2 tetapi memiliki magnitude lebih besar dari sinyal frekuensi f2 dan f3. Sedangkan spektrum sinyal f2 memiliki frekuensi lebih tinggi dibanding sinyal f1 tetapi lebih rendah dibanding dengan frekuensi sinyal f3. Magnitude sinyal f2 dan f3 adalah sama besar dan lebih kecil dibanding dengan magnitude sinyal f1.

Dari penjelasan Gambar 1 dan 2 dapat disimpulkan bahwa DFT dapat mengubah variabel-variabel sinyal pada domain waktu menjadi variabel dalam domain frekuensi sehingga sebuah sinyal tidak beraturan pada domain waktu dapat diketahu semua frekuensi pembentuk sinyal tak beraturan tersebut. Variabel variabel sinyal pada domain frekuensi beruba magnitude, sudut (fasa) dan frekuensi. 

Deret Fourier (Fourier Series)

Dalam matematika dan terutama bagi Anda yang belajar elektronika teori umumnya pernah membaca atau mendengar istilah Deret Fourier yang umumnya dituliskan sebagai berikut:

Maksud dari Deret Fourier di atas secara umum dapat dituliskan sebagai berikut :

Saat pada nilai t tertentu Deret Fourier di atas menyatakan ada atau tidaknya magnitude suatu sinyal pada nilai frekuensi terendah hingga frekuensi ke n (frekuensi tinggi).

Deret Fourier di atas dapat disederhanakan dalam penulisannya sebagai berikut:

Dimana nilai N secara teoritis adalah tidak terhingga. Dalam perhitungan untuk aplikasi yang digunakan pada kehidupan nyata perlu membatasi hingga nilai N tertentu.

A0 menyatakan nilai magnitude saat frekuensi 0 atau dapat dikatakan amplitudo komponen dc suatu sinyal. Kemudian bilangan selanjutnya setelah A0 adalah menyatakan magnitude sinyal saat frekuensi 1 kali, 2 kali, 3 kali hingga frekuensi yang ke n kali, dimana setiap nilai magnitude pada fungsi sin (Bn) dan cos (An) pada frekuensi tertentu dijumlahkan. Untuk menjumlahkan semua magnitude di atas tidak dapat dilakukan dengan penjumlahan biasa, akan tetapi dengan menjumlahkan masing-masing  magnitude secara vector pada fungsi sin dan cos yang umumnya ditulis dalam bentuk bilangan kompleks lalu dicari resultan-nya.

An merupakan koefisien dari fungsi cos atau bisa dikatakan merupakan magnitude maksimum dari fungsi sin. Untuk mendapatkan nilai ini perlu mengintegralkan fungsi cos pada saat nilai n tertentu. Bn merupakan koefisien dari fungsi sin atau dapat diasumsikan magnitude maksimum dari fungsi sin, dan untuk medapatkan nilai ini perlu mengintegralkan nilai fungsi sin saat nilai n tertentu.

Pada materi DFT ini tidak dibahas tentang bagaimana cara mencari koefisien An dan Bn karena fokus pada pemahaman DFT. Pada DFT, sebuah sinyal sinusoidal diasumsikan sebagai hasil penjumlahan sinyal fungsi cos dengan magnitude maksimum An dan fungsi sin dengan magnitude maksimum Bn.

Untuk penjelasan lebih teperinci menegenai DFT perlu memahami penjabaran dari penjumlahan fungsi sin dan cos yang umumnya dituliskan dalam bentuk bilangan kompleks yang dijelaskan pada materi di bawah ini.

Dasar Fungsi Sinyal

Hal mendasar untuk memahami DFT adalah memahami dasar teori sinyal yang digunakan pada DFT. Contoh sederhana fungsi sebuah sinyal ditunjukan pada Gambar 3.

Gambar 3. Ilustrasi fungsi sinyal dengan periode x

Gambar 3 di atas menunjukan 3 fungsi sinyal yang berbeda frekuensi dengan magnitude yang sama. Satu getaran sinyal atau gelombang dalam satu periode memiliki satu puncak dan satu lembah, dua getaran berarti memiliki dua puncak dan dua lembah dan seterusnya sehingga fungsi sinyal dalam Gambar 3 dapat dijabarkan sebagai berikut :

• Sinyal dengan fungsi f(x) = A sin x memiliki arti bahwa sinyal tersebut dalam satu periode x hanya memiliki satu getaran gelombang saja dengan magnitude maksimum sebesar A. 
• Sinyal dengan fungsi f(x) = A sin 2x  berarti dalam satu periode x memiliki 2 getaran gelombang atau sinyal dengan magnitude maksimum sinyal sebesar A.
• Sinyal dengan fungsi f(x) = A sin 3x  berarti dalam satu periode x memiliki 3 getaran gelombang atau sinyal dengan magnitude maksimum sinyal sebesar A.

Setelah memahami maksud dari dasar fungsi sinyal di atas, variabel x umumnya diganti dengan t karena fungsi berhubungan dengan waktu dan frekuensi, sehingga fungsi di atas dapat ditulis sebagai berikut :

Maksud dari persamaan di atas adalah suatu fungsi sinyal f(t) merupakan magnitude dari fungsi sin dengan satu periode putaran 2π dengan frekuensi f pada nilai t tertentu dengan magnitude maksimum adalah A.

Frekuensi juga dapat ditulis dalam bentuk nilai 1/T yang berarti banyaknya putaran atau getaran selama satu periode T. sehingga fungsi f(t) = A sin (2π f t) dapat ditulis sebagai berikut :

Dari penjelasan ilustrasi sinyal pada Gambar 3, maka sinyal dalam fungsi waktu ditunjukan oleh Gambar 4.

Gambar 4. Ilustrasi sinyal dalam fungsi waktu

Jika diubah menjadi kalimat maka fungsi sinyal di atas dapat dijabarkan sebagai berikut :

• f(t) = A sin (2π 1/T t) memiliki arti bahwa fungsi dalam satu periode memiliki sebuah siklus atau getaran sinyal dengan magnitude maksimum A.
• f(t) = A sin (2π 2/T t) memiliki arti bahwa fungsi dalam satu periode memiliki dua siklus atau dua getaran sinyal dengan magnitude maksimum A.
• f(t) = A sin (2π 3/T t) memiliki arti bahwa fungsi dalam satu periode memiliki tiga siklus atau tiga getaran sinyal dengan magnitude maksimum A.

Magnitude DFT

Dalam teori DFT sebuah fungsi suatu sinyal dapat dituliskan dalam bentuk bilangan kompleks yang terdiri dari komponen real dan komponen imaginary. Dengan nilai real dan imaginary dapat dicari nilai magnitude yang dapat dianalogikan sebagai amplitudo suatu sinyal pada frekuensi tertentu, selain itu juga dapat mengetahui fasa suatu sinyal.

Dasar pemahaman penulisan fungsi sinyal dalam bentuk kompleks dapat dilihat pada Gambar 5.

Gambar 5. Ilustrasi komponen real dan imaginary pada sebuah sinyal sinusoidal

Sebuah sinyal dengan fungsi f(t) = A sin (2π 1/T t) dapat diasumsikan merupakan penjumlahan fungsi sin dan cos pada sinyal berwarna biru seperti ditunjukan pada Gambar 5 yang dituliskan sebagai berikut :

Gambar 5 juga menunjukan diagram fasor yang menyatakan bahwa As merupakan vector komponen imaginary dengan nilai maksimum 1j atau sering ditulis j saja. Sedangkan Ac merupakan vector komponen real dimana magnitude maksimumnya adalah sama seperti nilai maksimum fungsi cos yaitu 1 sehingga fungsi sinyal dalam bilangan kompleks dapat dituliskan sebagai berikut :

Dari Gambar 5 dapat dilihat bahwa saat gelombang atau sinyal bergerak kearah sumbu t maka resultan vector real dan imaginary membentuk sudut θ dimana resultan bergerak berputar berlawanan arah jarum jam yang menyebabkan tanda positif (+) pada komponen imaginary fungsi sinyal berubah menjadi negatif (-) sehingga dapat dituliskan sebagai berikut :

Persamaan sinyal di atas dapat dituliskan menggunakan persamaan Euler sebagai berikut :

sehingga dapat dituliskan:

Dasar bilangan kompleks dan bentuk eksponensial di atas merupakan dasar rumus yang digunakan pada DFT.

DFT (Discrete Fourier Transform)

DFT merupakan penerapan dari deret Fourier yang telah dijelaskan di atas, hanya saja magnitude sinyal diambil pada waktu tertentu saja dan cukup singkat (diskrit). Pada penerapannya nilai ini merupakan nilai hasil sampling suatu sinyal menggunakan sebuah perangkat ADC (Analog to Digital Converter) kemudian diproses menggunakan rumus DFT menggunakan program yang ditulis pada sebuah komputer atau mikrokontroler.

Dasar Sampling sinyal untuk mengkonversi nilai kontinyu menjadi nilai diskrit

Sampling pada suatu sinyal dapat diasumsikan sebagai proses pengambilan nilai magnitude suatu sinyal saat waktu tertentu dan cukup singkat yang diulang terus menerus hingga batas waktu yang ditentukan atau selama periode tertentu. Dalam satu periode terdapat total sampel yang diambil dimana total sampel tersebut lebih dikenal dengan notasi N. Kecepatan yang dibutuhkan untuk mengambil maksimum jumlah sampel pada rentang waktu tertentu disebut sebagai frekuensi sampling rate atau sample rate. Syarat pengambilan sampel adalah frekuensi sampling minimal lebih besar atau sama dengan dua kali dari frekuensi sinyal informasi sehingga dapat ditulis sebagai berikut :

fs : Frekuensi sampling.

fi : Frekuensi informasi atau frekuensi sinyal.

Gambar 6. Ilustrasi pengambilan sampel (sampling) pada sebuah sinyal sinusoidal

Gambar 6 mengilustrasikan proses pengambilan sampel sebuah sinyal sinusoidal yang memiliki komponen dc. Angka urutan berwarna merah merupakan sampel ke n dimana banyaknya sampel ditulis dengan notasi N.

Dalam kondisi sebenarnya suatu sinyal bisa sangat panjang sekali atau tak terhingga contohnya sinyal sinusoidal listrik rumah tangga yang berasal dari perusahaan listrik. Untuk pengambilan sampel sinyal dengan periode tak terhingga sangatlah tidak mungkin, oleh karena itu perlu mengasumsikan sinyal sebagai sinyal dengan periode terbatas (finite) dengan jumlah sampel maksimum N. Dengan kata lain tetap melakukan pengambilan sampel dengan periode tak terhingga hanya saja dilakukan per segmen dengan periode dan jumlah sample N tertentu secara berulang-ulang. Dalam pengambilan sampel dengan jumlah sampel N juga perlu menentukan frekuensi sampling agar dapat membaca infomasi pada sinyal benar seperti tegangan, frekuensi dan fasa sinyal.

Rumus DFT

Dari penjelasan magnitude DFT, dasar fungsi sinyal serta deret Fourier di atas memberikan gambaran jelas maksud dari rumus DFT yang umum ditulis sebagai berikut :

dimana :

k : Indeks frekuensi yang menyatakan frekuensi ke k. Maksimum nilai k pada DFT adalah sama dengan nilai n. k adalah bilangan positif dimulai dari 0, 1, 2, ... dan seterusnya hingga N-1.

x(k) = merupakan magnitude atau merupakan resultan dari penjumlahan vector real dan imaginary pada saat indeks k.

n : Menyatakan sampel ke n dimana n adalah bilangan 0, 1, 2, ...dan seterusnya.

N : Menyatakan total atau banyaknya n.

x(n) : Merupakan nilai diskrit dari pengambilan sampel sinyal saat n. Salah satu contoh nilai diskrit ini adalah hasil pengambilan sampel suatu sinyal dari perangkat ADC yang dibaca oleh mikrokontroler atau komputer.

 : Merupakan bentuk eksponensial yang menyatakan penjumlahan vector real dan imaginary sebuah sinyal seperti dijelaskan pada Gambar 5 di atas.

Dalam mencari magnitude sinyal saat k tertentu yaitu dengan menjumlahkan semua vector pada saat k kemudian mencari resultan dari vector tersebut kemudian dirata-rata sebanyak N sampel sehingga magnitude sinyal dapat dituliskan sebagai berikut:

Beberapa literatur ada yang langsung menuliskan dalam bentuk DFT supaya menghasilkan magnitude sehingga umum ditulis sebagai berikut :

Dari rumus DFT di atas didapatkan nilai magnitude pada masing-masing nilai indeks frekuensi k dari nilai k sama dengan 0 hingga k sama dengan N - 1. Nilai magnitude X(k)  hanya dapat diambil nilainya saat k sama dengan 0 hingga k sama dengan N/2 - 1 karena saat k sama dengan N/2 - 1 hingga k sama dengan  N - 1 merupakan pencerminan dari nilai k sama dengan  0 hingga k sama dengan N/2 - 1. Pencerminan pada DFT lebih dekenal dengan sebutan efek folding, sehingga pencerminan hasil perhitungan  DFT dapat dituliskan sebagai berikut :

• X(k = 0) dianggap adalah nilai yang tidak memiliki frekuensi atau bisa dinyatakan sebagai komponen dc.
• X(k = 1) nilainya sama dengan X(k = N - 1)
• X(k = 2) nilainya sama dengan X(k = N - 2)
• X(k = 3) nilainya sama dengan X(k = N - 3)
• dan seterusnya hinga X(k = N/2 - 1) nilainya sama dengan X(k = N - (N/2 - 1))

Gambar 7 menunjukan hasil perhitungan nilai k DFT dari 0 hingga N - 1 yang menunjukan bahwa  nilai k = N/2 - 1  hingga N merupakan pencerminan dari nilai k = 0 hingga k = N/2 - 1. 

Gambar 7. Ilustrasi nikai k hasil perhitungan DFT dengan N = 8

 

Dari efek folding DFT ditunjukan Gambar 7 dapat disimpulan bahwa saat melakukan perhitungan DFT, hasil yang diambil hanya saat nilai k sama dengan 0 hingga k sama dengan N/2 - 1 seperti ditunjukan pada Gambar 8.

Gambar 8. Ilustrasi nilai k dengan 0 hingga k sama dengan N/2 - 1

Hasil perhitungan DFT belum menyatakan magnitude pada frekuensi sebenarnya karena X(k) menyatakan magnitude pada saat indek frekuensi k. Untuk mencari tahu frekuensi sebenarnya saat k, perlu mengalikan nilai indeks frekuensi k dengan frekuensi sampling DFT yang dibagi dengan banyaknya sampel sehingga dapat ditulis sebagai berikut : 

dimana :

k = indeks frekuensi

fs = frekuensi sampling

N = Jumlah atau banyaknya sampel

Jika diambil contoh frekuensi sampling 100 Hz dan jumlah sampel adalah 8 maka frekuensi setiap nilai k hingga k sama dengan N/2 - 1 adalah sebagai berikut :

• Saat k = 0, f = 0 . 100Hz / 8 = 0 Hz
• Saat k = 1, f = 1 . 100Hz / 8 = 12,5 Hz
• Saat k = 2, f = 2 . 100Hz / 8 = 25 Hz
• Saat k = 3, f = 3 . 100Hz / 8 = 37,5 Hz

Sehingga dengan jumlah sampel 8 maka frekuensi yang dapat dideteksi secara teoritis maksimum adalah 37.5 Hz sehingga nilai k pada Gambar 8 dapat diubah menjadi nilai frekuensi seperti ditunjukan pada Gambar 9.

Gambar 9. Ilustrasi magnitude hasil perhitungan DFT dengan k dikonversi menjadi frekuensi

Dari ilustrasi Gambar 9 dan perhitungan konversi k menjadi frekuensi dapat disimpulkan bahwa dengan memperbanyak nila N (sampel) dapat memberikan informasi frekuensi lebih teliti tetapi tetap saja informasi yang dapat diambil adalah pada saat k = 0 hingga k = N/2 - 1. Selain itu perlu diingat bahwa frekuensi sinyal informasi yang dapat diambil adalah sinyal informasi yang memiliki frekuensi setengah dari frekuensi sampling atau lebih kecil.

Untuk dapat mengimplementasikan DFT Anda perlu memenuhi beberapa hal dasar sebagai berikut :

1. Memahami konsep dasar DFT.
2. Memahami dasar pemahaman rangkaian elektronika.
3. Memahami dasar pemrograman yang akan digunakan misalnya python, atau C/C++.
4. Memiliki perangkat komputer yang memadai untuk DFT seperti mikrokontroler atau komputer.

Beberapa dasar langkah yang perlu dalam membuat program DFT adalah :

1. Menentukan frekuensi sampling serta menentukan jumlah sampel sesuai kebutuhan untuk mendapatkan informasi frekuensi yang diinginkan.
2.  Menyimpan semua hasil sampling and hold atau sampel yang didapatkan sebanyak N kedalam sebuah array data untuk kemudian diproses dalam perhitungan DFT.
3. Melakukan perhitungan DFT menggunakan rumus DFT dimana data pada array yang dikalikan dengan bilangan eksponensial DFT seperti rumus DFT yang dijelaskan di atas. Hasil DFT adalah magnitude dengan k =0 hingga k = N/2 - 1.
4. Melakukan pengubahan indeks frekuensi k dari k = 0 hingga k = N/2 -1.
5. Mem plot data saat indek k = 0 hingga k = N/2 -1 beserta magnitude yang dihasilkan pada saat nilai k tersebut dengan hasil plot k diganti dengan nilai frekuensi.

Secara umum DFT tidak cocok untuk aplikasi realtime karena DFT membutuhkan perhitungan yang membutuhkan waktu lebih (time lag). DFT sangat cocok digunakan untuk melakukan analisis terhadap suatu sinyal atau getaran atau lainnya karena dapat menunjukan spektrum frekuensi dalam suatu sinyal yang tidak bisa dilakukan pada domain waktu.

DFT juga sangat cocok untuk mengetahui getaran atau sinyal pada frekuensi rendah karena cukup presisi dan cukup mudah. Sedangkan untuk frekuensi yang tinggi kurang cocok karena membutuhkan CPU atau mikrokontroler dengan kecepatan tinggi, serta beberapa noise yang mungkin terjadi saat melakukan sample and hold.

Untuk mengembalikan sinyal dari perhitungan DFT (domain frekuensi) ke sinyal dalam domain waktu (kontinyu) dapat menggunakan IDFT (Inverse DFT) seperti persamaan di bawah ini.

EoF